Quantas bordas tem um prisma pentagonal?
Para poder contar Quantas bordas tem um prisma pentagonal?, os conceitos "borda" (borda de um objeto), "prisma" (figura geométrica) e "pentagonal" (relativo à forma de uma figura geométrica) devem ser entendidos.
Quando se fala de pentagonal, a primeira coisa a pensar é que o prefixo "penta" indica que a figura deve ter cinco lados. Portanto, a figura deve ter uma forma semelhante à de um pentágono.

Uma "aresta" é uma aresta de um objeto. Geometricamente, é uma linha que conecta dois vértices consecutivos de uma figura geométrica.
Um "prisma" é uma figura geométrica limitada por duas bases, que são polígonos iguais e paralelos, e cujas faces laterais são paralelogramos.
Na imagem mostrada no começo, as faces laterais do prisma pentagonal são retângulos. Este é apenas um caso particular, porque a definição indica que suas faces laterais são paralelogramos.
Isso permite que os prismas sejam classificados como "retos" e "oblíquos".

Para saber quantas bordas tem um prisma pentagonal, o tipo de prisma com o qual está trabalhando não importa. Seja direto ou oblíquo, o número de arestas não será alterado.
Formas de contar as arestas de um prisma pentagonal
1- Primeira forma
Como as bases dos prismas pentagonais são pentágonos, então cada base tem cinco arestas.
Por outro lado, de cada vértice de um pentágono, uma borda é projetada para o vértice correspondente do outro pentágono; isto é, há cinco arestas que unem uma base com a outra.
Adicionando todas as arestas, obtemos um total de 15 arestas.
2- Segunda forma
Outra maneira de contar as arestas é decompondo o prisma pentagonal em suas duas bases e suas faces laterais. Isto irá obter dois pentágonos e um paralelogramo com quatro linhas interiores.

Cada pentágono tem cinco arestas. Por outro lado, à primeira vista, pode-se cometer o erro de dizer que o paralelogramo contém oito arestas (seis verticais e duas horizontais). Mas esse raciocínio deve ser melhor analisado.
Se todas as linhas verticais forem contadas, é notável que a primeira linha à esquerda seja unida à última linha à direita, com a qual ambas as linhas representam uma única aresta. Mas e as duas linhas horizontais?
Quando todas as peças são reunidas novamente, as linhas horizontais serão unidas, cada uma, com as cinco bordas de cada pentágono. Por esse motivo, contá-las separadamente seria um erro.
Assim, o paralelogramo contém cinco arestas do prisma que, juntamente com as 10 arestas contadas no início, dão um total de 15 arestas.
Outros tipos de prisma
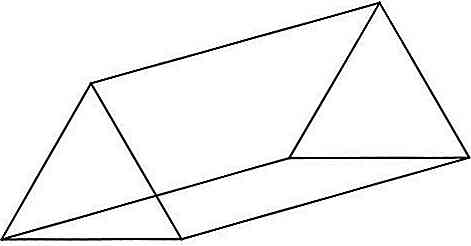
Prisma triangular
Estes são prismas nos quais as bases são triângulos e o número de arestas é 9.
 Prisma quadrangular
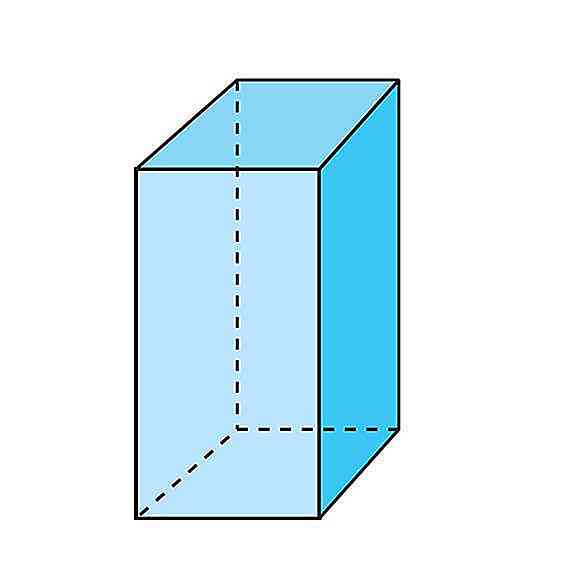
Prisma quadrangular
As bases desses prismas são quadriláteros e o número de arestas é 12.
 Prisma Hexagonal
Prisma Hexagonal
As bases são hexágonos e o número de arestas é 18.

Como pode ser visto nos outros tipos de prisma, o número de arestas pode ser deduzido através de uma fórmula matemática: seria igual a 3 multiplicado pelo número de lados que uma das bases possui.
Como foi dito antes, um prisma pode ser reto ou oblíquo, mas, além disso, existem prismas regulares e irregulares, além de prismas convexos e côncavos.

Referências
- Billstein, R., Libeskind, S., e Lott, J. W. (2013). Matemática: uma abordagem de resolução de problemas para professores de educação básica. López Mateos Editores.
- Fregoso, R. S., e Carrera, S. A. (2005). Matemática 3. Editorial de progresso.
- Gallardo, G., & Pilar, P. M. (2005). Matemática 6. Editorial de progresso.
- Gutiérrez, C. T., & Cisneros, M. P. (2005). Curso de Matemática 3º. Editorial de progresso.
- Kinsey, L. e Moore, T. E. (2006). Simetria, Forma e Espaço: Uma Introdução à Matemática Através da Geometria (ilustrado, editado por reimpressão). Springer Science & Business Media.
- Mitchell, C. (1999). Projetos de linha de matemática deslumbrante (Ed. Ilustrada). Scholastic Inc.
- R., M. P. (2005). Eu desenho 6º. Editorial de progresso.



 Prisma quadrangular
Prisma quadrangular Prisma Hexagonal
Prisma Hexagonal