Leis dos expoentes (com exemplos e exercícios resolvidos)
O leis de expoentes são aqueles que se aplicam àquele número que indica quantas vezes um número base deve ser multiplicado por si mesmo. Os expoentes também são conhecidos como poderes. A potenciação é uma operação matemática formada por uma base (a), o expoente (m) e a potência (b), que é o resultado da operação.
Os expoentes são geralmente usados quando quantidades muito grandes são usadas, porque elas não são mais do que abreviaturas que representam a multiplicação desse mesmo número um certo número de vezes. Os expoentes podem ser positivos e negativos.

Índice
- 1 Explicação das leis dos expoentes
- 1.1 Primeira lei: poder do expoente igual a 1
- 1.2 Segunda lei: potência do expoente igual a 0
- 1.3 Terceira lei: expoente negativo
- 1.4 Quarta lei: multiplicação de poderes com base igual
- 1.5 Quinta lei: divisão de poderes com base igual
- 1.6 Sexta lei: multiplicação de poderes com uma base diferente
- 1.7 Sétima lei: divisão de poderes com uma base diferente
- 1.8 Oitava lei: poder de uma potência
- 1.9 Nona lei: expoente fracionário
- 2 exercícios resolvidos
- 2.1 Exercício 1
- 2.2 Exercício 2
- 3 referências
Explicação das leis dos expoentes
Como dito acima, os expoentes são uma forma abreviada que representa a multiplicação de números por si mesmos várias vezes, onde o expoente é relacionado apenas ao número à esquerda. Por exemplo:
23 = 2*2*2 = 8
Nesse caso, o número 2 é a base da potência, que será multiplicada 3 vezes conforme indicado pelo expoente, localizado no canto superior direito da base. Existem diferentes maneiras de ler a expressão: 2 aumentadas para 3 ou também 2 para o cubo.
Os expoentes também indicam o número de vezes que podem ser divididos e, para diferenciar essa operação da multiplicação, o expoente carrega o sinal de menos (-) na frente dela (é negativo), o que significa que o expoente está no denominador de um fração. Por exemplo:
2- 4 = 1/ 2*2*2*2 = 1/16
Isso não deve ser confundido com o caso em que a base é negativa, pois dependerá se o expoente é par ou ímpar para determinar se a potência será positiva ou negativa. Então você tem que:
- Se o expoente é par, a potência será positiva. Por exemplo:
(-7)2 = -7 * -7 = 49.
- Se o expoente for ímpar, a potência será negativa. Por exemplo:
(-2)5 = (-2)*(-2)*(-2)*(-2)*(-2)=-32.
Há um caso especial em que se o expoente for igual a 0, a potência é igual a 1. Existe também a possibilidade de que a base seja 0; Nesse caso, dependendo do exposto, a potência será indeterminada ou não.
Para realizar operações matemáticas com os expoentes, é necessário seguir várias regras ou regras que facilitam encontrar a solução para essas operações.
Primeira lei: poder expoente igual a 1
Quando o expoente é 1, o resultado será o mesmo valor da base:1 = a.
Exemplos
91 = 9.
221 = 22.
8951 = 895.
Segunda lei: potência do expoente igual a 0
Quando o expoente é 0, se a base for diferente de zero, o resultado será :, um0 = 1.
Exemplos
10 = 1.
3230=1.
10950 = 1.
Terceira lei: expoente negativo
Como a exponencial é negativa, o resultado será uma fração, onde a potência será o denominador. Por exemplo, se m é positivo, então um-m= 1 / am.
Exemplos
- 3-1 = 1/ 3.
- 6-2 = 1 / 62 = 1/36.
- 8-3 = 1/ 83 = 1/512.
Quarta lei: multiplicação de poderes com base igual
Para multiplicar poderes onde as bases são iguais e diferentes de 0, a base é mantida e os expoentes são adicionados:m * umn = am + n.
Exemplos
- 44 * 43 = 44+3 = 47
- 81 * 84 = 81+4 = 85
- 22 * 29 = 22+9 = 211
Quinta lei: divisão de poderes com base igual
Para dividir potências nas quais as bases são iguais e diferentes de 0, a base é mantida e os expoentes são subtraídos como segue:m / an = am-n.
Exemplos
- 92 / 91 = 9 (2 - 1) = 91.
- 615 / 610 = 6 (15 - 10) = 65.
- 4912 / 496 = 49 (12 - 6) = 496.
Sexta lei: multiplicação de poderes com uma base diferente
Nesta lei, temos o oposto do que é expresso no quarto; isto é, se existem bases diferentes com expoentes iguais, as bases são multiplicadas e o expoente é mantido:m * bm = (a*b) m.
Exemplos
- 102 * 202 = (10 * 20)2 = 2002.
- 4511 * 911 = (45*9)11 = 40511.
Outra maneira de representar esta lei é quando a multiplicação é elevada a um poder. Assim, o expoente pertencerá a cada um dos termos: (a*b)m= am* bm.
Exemplos
- (5*8)4 = 54 * 84 = 404.
- (23 * 7)6 = 236 * 76 = 1616.
Sétima lei: divisão de poderes com base diferente
Se houver bases diferentes, mas com expoentes iguais, as bases são divididas e o expoente é mantido:m / bm = (a / b)m.
Exemplos
- 303 / 23 = (30/2)3 = 153.
- 4404 / 804 = (440/80)4 = 5,54.
Da mesma forma, quando uma divisão é elevada a um poder, o expoente pertencerá a cada um dos termos: (a / b) m = am / bm.
Exemplos
- (8/4)8 = 88 / 48 = 28.
- (25/5)2 = 252 / 52 = 52.
Há um caso em que o expoente é negativo. Então, para ser positivo, o valor do numerador é invertido com o do denominador, da seguinte maneira:
- (a / b)-n = (b / a)n = bn / an.
- (4/5) -9 = ( 5 / 4) 9 = 59 / 44.
Oitava lei: poder de um poder
Quando você tem um poder que é elevado a outro poder - isto é, dois expoentes ao mesmo tempo -, a base é mantida e os expoentes se multiplicam:m)n= am *n.
Exemplos
- (83)2 = 8 (3*2) = 86.
- (139)3 = 13 (9*3) = 1327.
- (23810)12 = 238(10 * 12) = 238120.
Nona lei: expoente fracionário
Se o poder tiver uma fração como um expoente, ele será resolvido transformando-o em uma enésima raiz, onde o numerador permanece como um expoente e o denominador representa o índice da raiz:
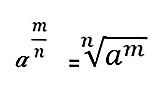 Exemplo
Exemplo

Exercícios resolvidos
Exercício 1
Calcule as operações entre os poderes que possuem bases diferentes:
24 * 44 / 82.
Solução
Aplicando as regras dos expoentes, no numerador as bases são multiplicadas e o expoente é mantido, assim:
24 * 44 / 82=(2*4)4 / 82 = 84 / 82
Agora, como temos as mesmas bases, mas com expoentes diferentes, a base é mantida e os expoentes são subtraídos:
84 / 82 = 8(4 - 2) = 82
Exercício 2
Calcule as operações entre as altas potências para outra potência:
(32)3 * (2 * 65)-2 * (22)3
Solução
Aplicando as leis, você precisa:
(32)3 * (2 * 65)-2 * (22)3
=36 * 2-2 * 2-10 * 26
=36 * 2(-2) + (- 10) * 26
=36 * 2-12 * 26
=36 * 2(-12) + (6)
=36 * 26
=(3*2)6
=66
=46.656
Referências
- Aponte, G. (1998). Fundamentos da Matemática Básica. Educação Pearson.
- Corbalán, F. (1997). Matemática aplicada à vida cotidiana.
- Jiménez, J. R. (2009). Matemática 1 SET.
- Max Peters, W. L. (1972). Álgebra e trigonometria
- Rees, P. K. (1986). Reverte



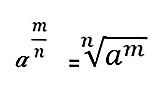 Exemplo
Exemplo