Composição, tipos e exemplos de transformações isométricas

O Transformações isométricas são mudanças de posição ou orientação de uma certa figura que não alteram nem a forma nem o tamanho dela. Essas transformações são classificadas em três tipos: translação, rotação e reflexão (isometria). Em geral, as transformações geométricas permitem criar uma nova figura a partir de outra dada.

Uma transformação em figura geométrica significa que, de alguma forma, foi submetida a alguma mudança; isto é, que foi alterado. De acordo com o sentido do original e do similar no plano, as transformações geométricas podem ser classificadas em três tipos: isométricas, isomórficas e anamórficas.

Índice

• 1 caraterísticas
• 2 tipos
  • 2.1 Por tradução
  • 2.2 Por rotação
  • 2.3 Por reflexão ou simetria
• 3 Composição
  • 3.1 Composição de uma tradução
  • 3.2 Composição de uma rotação
  • 3.3 Composição de uma simetria
• 4 referências

Características

Transformações isométricas ocorrem quando as magnitudes dos segmentos e os ângulos entre o original e a figura transformada são preservados.

Neste tipo de transformação, nem a forma nem o tamanho da figura são alterados (são congruentes), é apenas uma mudança de posição da figura, seja na orientação ou na direção. Desta forma, os números inicial e final serão semelhantes e geometricamente congruentes.

Isometria refere-se à igualdade; isto é, que as figuras geométricas serão isométricas se tiverem a mesma forma e tamanho.

Nas transformações isométricas, a única coisa que pode ser observada é uma mudança de posição no plano, um movimento rígido ocorre graças ao qual a figura muda de uma posição inicial para uma posição final. Essa figura é chamada homóloga (semelhante) ao original.

Existem três tipos de movimentos que classificam uma transformação isométrica: translação, rotação e reflexão ou simetria.

Tipos

Por tradução

São aquelas isometrias que permitem mover em linha reta todos os pontos do plano em uma determinada direção e distância.

Quando uma figura é transformada pela tradução, ela não muda sua orientação em relação à posição inicial, nem perde suas medidas internas, as medidas de seus ângulos e lados. Este tipo de deslocamento é definido por três parâmetros:

- Uma direção, que pode ser horizontal, vertical ou oblíqua.

- Um sentido, que pode ser para a esquerda, para a direita, para cima ou para baixo.

- Distância ou magnitude, que é o comprimento da posição inicial até o final de qualquer ponto que se mova.

Para uma transformação isométrica por tradução a ser cumprida, ela deve atender às seguintes condições:

- A figura deve manter sempre todas as suas dimensões, lineares e angulares.

- A figura não altera sua posição em relação ao eixo horizontal; isto é, seu ângulo nunca varia.

- As traduções serão sempre resumidas em uma, independentemente do número de traduções feitas.

Em um plano onde o centro é um ponto O, com coordenadas (0,0), a translação é definida por um vetor T (a, b), que indica o deslocamento do ponto inicial. Quer dizer:

P (x, y) + T (a, b) = P '(x + a, y + b)

Por exemplo, se uma tradução T (-4, 7) é aplicada ao ponto de coordenada P (8, -2), obtemos:

P (8, -2) + T (-4, 7) = P '[(8 + (-4)), ((-2) + 7)] = P' (4, 5)

Na imagem a seguir (à esquerda) pode-se observar como o ponto C foi movido até coincidir com D. Ele o fez na direção vertical, a direção foi para cima e a distância ou magnitude do CD foi de 8 metros. Na imagem direita, observa-se a translação de um triângulo:

Por rotação

São aquelas isometrias que permitem que a figura gire todos os pontos de um plano. Cada ponto gira seguindo um arco que tem um ângulo constante e um ponto fixo (centro de rotação) determinado.

Ou seja, toda rotação será definida pelo seu centro de rotação e ângulo de rotação. Quando uma figura é transformada por rotação, ela mantém a medida de seus ângulos e lados.

A rotação ocorre em uma determinada direção, é positiva quando a rotação é no sentido anti-horário (ao contrário de como as mãos do relógio giram) e negativa quando sua rotação é no sentido horário.

Se um ponto (x, y) é girado em relação à origem - isto é, seu centro de rotação é (0,0) -, em um ângulo de 90^o para 360^o As coordenadas dos pontos serão:

No caso em que a rotação não tem centro na origem, a origem do sistema de coordenadas deve ser transferida para a nova origem determinada, a fim de poder girar a figura tendo a origem como seu centro.

Por exemplo, se uma rotação de 90 é aplicada ao ponto P (-5,2)^o, em torno da origem e em um sentido positivo, suas novas coordenadas serão (-2,5).

Por reflexão ou simetria

São essas transformações que invertem os pontos e figuras do plano. Este investimento pode ser em relação a um ponto ou também pode ser em relação a uma linha.

Em outras palavras, neste tipo de transformação, cada ponto da figura original é associado a outro ponto (imagem) da figura homóloga, de tal forma que o ponto e sua imagem estejam na mesma distância de uma linha chamada eixo de simetria. .

Assim, a parte esquerda da figura será um reflexo da parte direita, sem alterar sua forma ou suas dimensões. A simetria transforma uma figura em outra, embora na direção oposta, como pode ser visto na imagem a seguir:

A simetria está presente em muitos aspectos, como em algumas plantas (girassóis), animais (pavão) e fenômenos naturais (flocos de neve). O ser humano reflete isso em seu rosto, que é considerado como um fator de beleza. A reflexão ou simetria pode ser de dois tipos:

Simetria central

É essa transformação que ocorre em relação a um ponto, no qual a figura pode mudar sua orientação. Cada ponto da figura original e sua imagem estão na mesma distância de um ponto O, chamado de centro de simetria. A simetria é central quando:

- Tanto o ponto quanto sua imagem e centro pertencem à mesma linha.

- Com uma rotação de 180^o do centro O você obtém um valor igual ao original.

- Os traços da figura inicial são paralelos aos traços da figura formada.

- O sentido da figura não muda, será sempre no sentido horário.

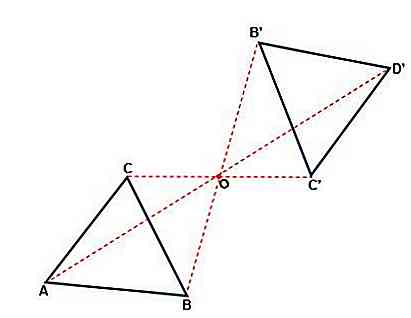Simetria axial

Essa transformação ocorre em relação ao eixo de simetria, onde cada ponto da figura inicial está associado a outro ponto da imagem e estes estão à mesma distância do eixo de simetria. A simetria é axial quando:

- O segmento que une um ponto à sua imagem é perpendicular ao seu eixo de simetria.

- As figuras mudam de direção em relação ao giro ou no sentido horário.

- Ao dividir a figura com uma linha central (eixo de simetria), uma das metades resultantes corresponde completamente a outra das metades.

Composição

Uma composição de transformações isométricas refere-se à aplicação sucessiva de transformações isométricas na mesma figura.

Composição de uma tradução

A composição de duas traduções resulta em outra tradução. Quando realizado no plano, no eixo horizontal (x) somente as coordenadas desse eixo mudam, enquanto as coordenadas do eixo vertical (y) permanecem as mesmas, e vice-versa.

Composição de uma rotação

A composição de duas voltas com o mesmo centro resulta em outra volta, que tem o mesmo centro e cuja amplitude será a soma das amplitudes das duas voltas.

Se o centro das voltas tiver um centro diferente, o corte da bissetriz de dois segmentos de pontos similares será o centro de rotação.

Composição de uma simetria

Nesse caso, a composição dependerá de como ela é aplicada:

- Se a mesma simetria for aplicada duas vezes, o resultado será uma identidade.

- Se duas simetrias forem aplicadas em relação a dois eixos paralelos, o resultado será uma translação e seu deslocamento será o dobro da distância desses eixos:

- Se duas simetrias forem aplicadas em relação a dois eixos que são cortados no ponto O (centro), será obtida uma rotação com o centro em O e seu ângulo será o dobro do ângulo formado pelos eixos:

Referências

1. V Burgués, J. F. (1988). Materiais para construir geometria. Madri: síntese.
2. Cesar Calavera, I. J. (2013). Desenho Técnico II. Paraninfo S.A: Ediciones de la Torre.
3. Coxeter, H. (1971). Fundamentos da Geometria. México: Limusa-Wiley.
4. Coxford, A. (1971). Geometria Uma Abordagem de Transformação. EUA: irmãos Laidlaw.
5. Liliana Siñeriz, R. S. (2005). Indução e formalização no ensino das transformações rígidas no ambiente CABRI.
6. P. J. (1996). O grupo de isometrias planas. Madri: síntese.
7. Suárez, A. C. (2010). Transformações no plano. Gurabo, Porto Rico: AMCT.