Teorema de Thales de Mileto primeiro, segundo e exemplos

O primeiro e o segundo Teorema de Thales de Mileto eles são baseados na determinação de triângulos de outros similares (primeiro teorema) ou circunferências (segundo teorema). Eles têm sido muito úteis em várias áreas. Por exemplo, o primeiro teorema mostrou-se muito útil para medir grandes estruturas quando não havia instrumentos de medição sofisticados.

Tales de Mileto foi um matemático grego que forneceu grandes contribuições para a geometria, da qual se destacam esses dois teoremas (em alguns textos eles também o escrevem como Thales) e suas aplicações úteis. Estes resultados foram utilizados ao longo da história e permitiram resolver uma grande variedade de problemas geométricos.

Índice

• 1 Primeiro Teorema dos Contos
  • 1.1 Aplicação
  • 1.2 Exemplos
• 2 Segundo Teorema dos Contos
  • 2.1 Aplicação
  • 2.2 Exemplo
• 3 referências

Primeiro teorema de contos

O primeiro teorema de Tales é uma ferramenta muito útil que, entre outras coisas, permite construir um triângulo similar ao outro, previamente conhecido. A partir disso são derivadas várias versões do teorema que podem ser aplicadas em múltiplos contextos.

Antes de dar sua declaração, lembre-se de algumas noções de similaridade de triângulos. Essencialmente, dois triângulos são semelhantes se seus ângulos são congruentes (eles têm a mesma medida). Isso dá origem ao fato de que, se dois triângulos são semelhantes, seus lados correspondentes (ou homólogos) são proporcionais.

O primeiro teorema de Thales afirma que, se em um dado triângulo, uma linha reta é traçada paralelamente a qualquer dos seus lados, o novo triângulo obtido será semelhante ao triângulo inicial.

Na figura anterior, os triângulos ABC e DEC são semelhantes. A proporcionalidade que é obtida devido a essa semelhança também dá origem a uma relação de proporcionalidade entre os dois lados do mesmo triângulo e os dois lados correspondentes do outro. Por exemplo, tendo em conta a figura anterior, você também teria que:Outra maneira em que você pode ver o primeiro teorema de Thales, e que também é muito útil, é isto: se duas linhas L1 e L2 (qualquer) são cortadas por linhas paralelas (qualquer número delas), então os segmentos formados em L1 são proporcionais aos correspondentes formados em L2.

Você também obtém uma relação entre os ângulos formados, como mostra a figura a seguir.

Aplicação

Entre suas múltiplas aplicações destaca-se um de particular interesse e tem a ver com uma das maneiras em que as medições foram feitas de grandes estruturas na antiguidade, tempo em que Thales viveu e em que os dispositivos de medição modernos não estavam disponíveis. Eles existem agora.

Dizem que é assim que Thales conseguiu medir a pirâmide mais alta do Egito, Quéops. Para isso, Thales supôs que os reflexos dos raios solares tocavam o chão formando linhas paralelas. Sob essa suposição, ele enfiou um bastão ou bengala no chão.

Então ele usou a similaridade dos dois triângulos resultantes, um formado pelo comprimento da sombra da pirâmide (que pode ser facilmente calculada) e a altura da pirâmide (o desconhecido), e o outro formado pelos comprimentos da sombra. e a altura da haste (que também pode ser facilmente calculada).

Usando a proporcionalidade entre esses comprimentos, você pode limpar e saber a altura da pirâmide.

Embora este método de medição possa dar um erro significativo de aproximação em relação à precisão da altura e depende do paralelismo dos raios solares (que por sua vez depende de um tempo preciso), devemos reconhecer que é uma ideia muito engenhosa. e isso proporcionou uma boa alternativa de medição para o tempo.

Exemplos

Encontre o valor de x em cada caso:

Primeiro caso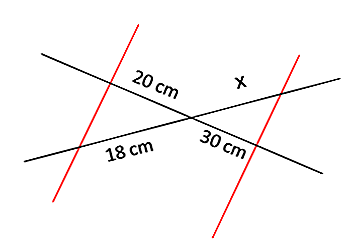 

Solução

Aqui temos duas linhas cortadas por duas linhas paralelas. Pelo primeiro teorema de Thales se tem que seus respectivos lados são proporcionais. Em particular:

Segundo caso

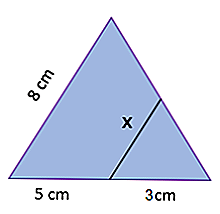
Solução

Aqui temos dois triângulos, um deles formado por um segmento paralelo a um dos lados do outro (precisamente o lado do comprimento x). Pelo primeiro teorema de Tales você tem que:

Segundo teorema dos contos

O segundo teorema de Thales determina um triângulo retângulo inscrito em uma circunferência em cada ponto do mesmo.

Um triângulo inscrito em uma circunferência é um triângulo cujos vértices estão na circunferência, estando assim contidos neste.

Especificamente, o segundo teorema de Thales afirma o seguinte: dado um círculo de centro O e diâmetro AC, cada ponto B da circunferência (diferente de A e C) determina um triângulo retângulo ABC, com ângulo reto. <>

A título de justificação, note que tanto OA quanto OB e OC correspondem ao raio da circunferência; Portanto, suas medições são as mesmas. A partir daí obtém-se que os triângulos OAB e OCB são isósceles, onde

Sabe-se que a soma dos ângulos de um triângulo é igual a 180º. Usando isso com o triângulo ABC você precisa:

2b + 2a = 180º.

Equivalentemente, temos que b + a = 90º eb + a =

Note que o triângulo retângulo fornecido pelo segundo teorema de Thales é precisamente aquele cuja hipotenusa é igual ao diâmetro da circunferência.Portanto, é completamente determinado pelo semicírculo que contém os pontos do triângulo; neste caso, o semicírculo superior.

Note também que no triângulo retângulo obtido por meio do segundo teorema de Thales, a hipotenusa é dividida em duas partes iguais por OA e OC (o raio). Por sua vez, esta medida é igual ao segmento OB (também o raio), que corresponde à mediana do triângulo ABC por B.

Em outras palavras, o comprimento da mediana do triângulo retângulo correspondente ao vértice B é completamente determinado pela metade da hipotenusa. Lembre-se de que a mediana de um triângulo é o segmento de um dos vértices até o ponto médio do lado oposto; neste caso, o segmento BO.

Circunferência circunscrita

Outra maneira de ver o segundo teorema de Thales é através de um círculo circunscrito a um triângulo retângulo.

Em geral, um círculo circunscrito a um polígono consiste na circunferência que passa por cada um dos seus vértices, sempre que for possível rastreá-lo.

I, utilizando o segundo teorema Tal dado um triângulo rectângulo, que pode sempre construir um círculo circunscrito a esta, de raio igual a metade da hipotenusa e circuncentro (o centro do círculo) como o ponto médio da hipotenusa.

Aplicação

Uma aplicação muito importante do segundo teorema Tal, e talvez o mais utilizado, é de encontrar as linhas tangentes a uma circunferência dado, por um ponto P externo para o (conhecido).

Note-se que dada uma circunferência (desenhada em azul na figura abaixo) e um ponto exterior P, existem duas tangentes à circunferência que passa através P. Sean T e T 'os pontos de tangência, r o raio do círculo e Ou o centro.

Sabe-se que o segmento que vai do centro de um círculo a um ponto de tangência é perpendicular a essa linha tangente. Então, o ângulo OTP é reto.

Pelo que vimos anteriormente no primeiro teorema de Thales e suas diferentes versões, vemos que é possível inscrever o triângulo OTP em outra circunferência (em vermelho).

Analogamente, obtém-se que o triângulo OT'P pode ser inscrito dentro da mesma circunferência anterior.

Para o segundo teorema adição Tal obtém-se o novo diâmetro do círculo é precisamente a hipotenusa do triângulo OTP (que é igual a hipotenusa do triângulo OT'P), e o centro é o ponto médio deste hipotenusa.

Para calcular o centro do círculo novo suficiente, então calcular o ponto médio entre o centro da circunferência-M- dizer inicial (já conhecido) e o ponto P (também conhecido). Então, o raio será a distância entre este ponto M e P.

Com o raio e o centro do círculo vermelho podemos encontrar sua equação cartesiana, a qual nos lembramos é dada por (x-h)² + (y-k)² = c², onde c é o raio e o ponto (h, k) é o centro do círculo.

Conhecendo agora as equações de ambas as circunferências, podemos interceptá-las resolvendo o sistema de equações formado por elas e, assim, obtendo os pontos de tangência T e T '. Finalmente, para conhecer as linhas tangentes desejadas, é suficiente encontrar a equação das linhas retas que passam por T e P, e por T 'e P.

Exemplo

Considere uma circunferência de diâmetro AC, centro O e raio 1 cm. Seja B um ponto na circunferência de tal forma que AB = AC. Quanto mede a AB?

Solução

Para o segundo teorema temos Tal triângulo ABC é rectângulo e a hipotenusa corresponde ao diâmetro, que neste caso é de 2 cm (o raio é de 1 cm). Então, pelo teorema de Pitágoras temos que:

Referências

1. Ana Lira, P. J. (2006). Geometria e Trigonometria. Zapopan, Jalisco: edições limítrofes.
2. Goodman, A. e Hirsch, L. (1996). Álgebra e trigonometria com geometria analítica. Educação Pearson.
3. Gutiérrez, Á. Á. (2004). Metodologia e aplicações da matemática no E.S.O. Ministério da Educação.
4. IGER. (2014). Matemática Segundo Semestre Zaculeu. Guatemala: IGER.
5. José Jiménez, L. J. (2006). Matemática 2. Zapopan, Jalisco: edições limítrofes.
6. M., S. (1997). Trigonometria e Geometria Analítica. Educação Pearson.
7. Pérez, M. A. (2009). Uma História da Matemática: Desafios e conquistas através de seus personagens. Livros de visão editorial.
8. Viloria, N., & Leal, J. (2005). Geometria Analítica Plana. Editorial venezuelano C.